简介:包括线性时间算法,最长递增子序列,以斐波那契堆实现迪杰斯特拉算法
1. 线性时间选择(序数问题)
- 问题描述:已知n个数,找出排序后第k小的数。要求平均时间复杂度为O(n)。
- 解决思路:使用快速排序的思想解决查找问题,用随机数(舍伍德算法)解决基准问题,用分治策略搭建整体的算法结构。
- 步骤分析:
(1) 使用舍伍德算法选择基准r(第r个数)
(2) 用快速排序算法进行下面的操作:将大于基准的数值放于基准后,将小于基准的数值放于基准前,刷新数组的排序。
(3) 若想要查找的第k个数值的k比基准r大,则取数组的右边再重复进行以上操作,若小于,则选择左边的,若等于,则输出。 - 示例:
示例分析:输入10个数,分别为5 2 7 8 9 0 1 3 4 6,第5小的元素为4,验证成功。
2. 最长递增子序列问题
- 问题描述:寻找最长递增的序列。
- 解决思路:利用矩阵记录之前的结果,用动态规划法完成寻找
- 算法步骤:
(1) 设置变量有:存储当前最长序列的值的数组tempmax,存储最长序列长度maxlen存储最长序列的最大值下标maxindex
(2) 从下标为1的值开始遍历
(3) 若i下标下的值比前一个值大,则更新tempmax[i]=tempmax[i-1]+1,即增加长度1,若此时的tempmaxp[i]比maxlen大,则更新maxlen,且更新maxindex=1 - 示例:
示例分析:输入10个数分别为1 3 2 4 5 3 7 8 9 6,其最长递增子序列为3 7 8 9,长度为4,验证成功。
3. 斐波那契堆实现最短路径算法(迪杰斯特拉)
- 问题描述:用斐波那契堆取最小路径辅助迪杰斯特拉算法实现最小路径算法
- 解决思路:1. 使用贪心算法实现迪杰斯特拉最短路径算法,使用斐波那契堆建立最小堆,方便取最小‘结点’以完成接下来的操作
- 算法思想:
迪杰斯特拉伪代码:
1
2
3
4
5
6
7
8
9DIJKSTRA(G, w, s)
INITIALIZE - SINGLE - SOURCE(G, s)
S ← Ø
Q ← V[G] //第3行,INSERT操作,O(1)构造堆
while Q ≠ Ø
do u ← EXTRACT - MIN(Q) //第5行,从堆中取出最小点
S ← S ∪{ u }
for each vertex v ∈ Adj[u]
do RELAX(u, v, w) //第8行,RELAX操作,对堆进行降级工作其中在第5行的EXTRACT-MIN操作用斐波那契堆实现,斐波那契堆结构如下:
- 斐波那契堆是由一组最小堆有序树构成的。每个节点的度数为其子节点的数目。树的度数为其根节点的度数。
- 斐波那契堆中的树都是有根的但是无序。每个节点x包含指向父节点的指针p[x]和指向任意一个子结点的child[x]。x的所有子节点都用双向循环链表链接起来,叫做x的子链表。子链表中的每一个节点y都有指向它的左兄弟的left[y]和右兄弟的right[y]。如果节点y是x仅有的子节点,则left[y]=right[y]=y。
- 斐波那契堆中所有树的根节点也用一个双向循环链表链接起来。使用一个指针指向斐波那契堆中最小元素。
用稀疏矩阵表示图,定义为weight
具体实现示例分析:
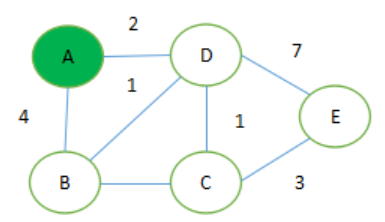
其矩阵如:
{0,4,NoEdge,2,NoEdge},
{4,0,4,1,NoEdge},
{NoEdge,4,0,1,3},
{2,1,1,0,7},
{NoEdge,NoEdge,3,7,0}
最终应该得到结果:
a->a=0
a->d->b=3
a->d->c=3
a->d=2
a->d->c->e=6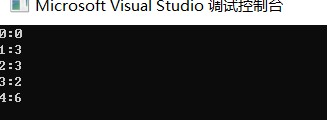
测试成功!